8 Jenis Pola Bilangan Matematika dan Rumusnya

Pola bilangan sering kali ditemui dalam kehidupan sehari-hari untuk memperkirakan sesuatu. Mulai dari nomor rumah, pelat nomor ganjil genap, hitung-hitungan jualan, dan banyak lagi.

Bilangan berpola tentunya tidak lepas dari sejumlah angka-angka yang dikelompokkan menjadi beberapa bagian.

Lihat Juga : Rumus Bangun Datar Lengkap untuk Menghitung Luas dan Keliling

Dirangkum dari buku Be Smart Matematika, berikut ini pengertian pola bilangan, jenis, dan rumusnya.

Apa Itu Pola Bilangan?

Pola bilangan adalah deretan angka yang mempunyai aturan tersendiri dalam penyusunannya sehingga membentuk suatu pola.

Pada setiap bilangan yang sudah tersusun menjadi pola, memiliki bentuk perhitungan atau rumus berbeda-beda.

Jenis Pola Bilangan dan Rumusnya

Jenis-jenis pola bilangan ada banyak, di bawah ini daftar dan rumusnya yang perlu kamu tahu.

1. Pola bilangan asli

Pola bilangan asli mulai tersusun dari angka 1 sampai tak hingga, seperti 1,2,3,4,5,6,7,8,9,10... dan seterusnya.

Rumus: n, di mana (n) ini adalah bilangan asli.

2. Pola bilangan genap

Pola bilangan genap terdiri dari bilangan genap yang habis dibagi 2. Contohnya 2,4,6,8,10,12,14... dan seterusnya.

Rumus: 2n, di mana (n) ini adalah bilangan asli.

3. Pola bilangan ganjil

Pola bilangan ganjil mempunyai susunan bilangan yang tak habis dibagi 2, yaitu 1,3,5,7,9,11,13...dan seterusnya.

Rumus: 2n-1, (n) ini adalah bilangan asli.

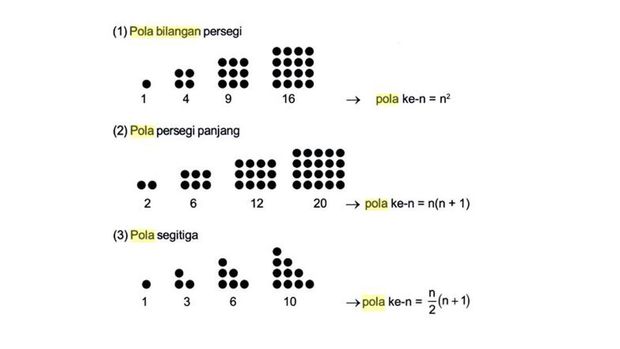
4. Pola bilangan persegi

Ilustrasi. Jenis pola bilangan matematika dan rumusnya, rumus pola bilangan persegi (Arsip Google Books Kupas Matematika SMA untuk kelas 1, 2, & 3)

Pola bilangan persegi berarti susunan bilangannya bisa membentuk persegi. Contohnya 1,4,9,16...dan seterusnya.

Rumus: pola ke-n=n2

5. Pola bilangan persegi panjang

Tidak beda jauh dengan persegi, pola bilangan persegi panjang juga susunannya menyerupai bangun datar persegi panjang. Contohnya 2,6,12,20...dan seterusnya.

Rumus: pola ke-n= n(n+1)

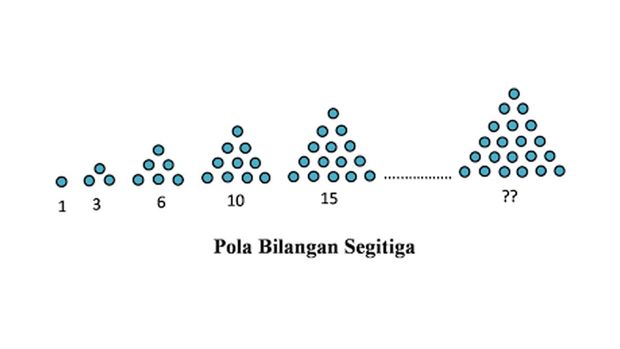
6. Pola bilangan segitiga

Ilustrasi. Jenis pola bilangan matematika dan rumusnya, rumus pola bilangan segitiga (Arsip Google Books Kupas Matematika SMA untuk kelas 1, 2, & 3)

Sesuai namanya, pola bilangan yang satu ini akan membentuk bangun segitiga sama sisi. Contoh bilangannya 1,3,6,10...dan seterusnya.

Rumus: pola ke-n= n (n+1)
                                 2

7. Pola bilangan segitiga pascal

Bilangan segitiga pascal ini terbilang unik karena ada beberapa ketentuan tersendiri untuk membentuk pola, di antaranya:

• Baris paling atas ditulis satu kotak saja yaitu 1 (satu).
• Setiap baris dalam segitiga pascal selalu diawali dan diakhiri angka 1.
• Jumlah kotak selanjutnya dalam segitiga pascal ditulis di baris ke-2 sampai ke-n, yaitu hasil penjumlahan dua bilangan diagonal di atasnya.
• Setiap baris akan membentuk simetris.
• Banyak bilangan di setiap barisnya memiliki kelipatan dua dari jumlah angka baris sebelumnya.

Barisan bilangan segitiga pascal terdiri dari 1,2,4,8,16...dan seterusnya.

Rumus: n2-1 di mana (n) ini bilangan asli.

8. Pola bilangan fibonacci

Bilangan fibonacci merupakan susunan bilangan yang berawalan dari 0 dan 1. Bilangan ini diperoleh dengan menambahkan suku angka dari jumlah dua suku sebelumnya.

Contohnya: 1,1,2 (dua ini hasil penambahan dari 1 dan 1 di suku sebelumnya), 3 (tiga ini hasil penambahan dari 1 dan 2 di suku sebelumnya), 5 (lima ini hasil penambahan dari 2 dan 3 di suku sebelumnya), 8 (delapan ini hasil penambahan dari 3 dan 5 di suku sebelumnya).

Jika digambarkan secara hasil, maka bentuk pola bilangan fibonacci seperti berikut: 1,1,2,3,5,8,13...dan seterusnya.

Lihat Juga : Pengertian, Sifat, dan Jenis Bilangan Asli

Demikian jenis pola bilangan matematika dan rumusnya. Semoga dapat bermanfaat.